树 —— 十年树木百年修BUG

二叉查找树（Binary Search Tree）

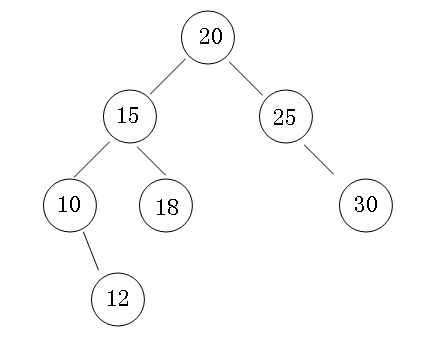
也称为二叉搜索树、有序二叉树（ordered binary tree）或排序二叉树（sorted binary tree），是指一棵空树或者具有下列性质的二叉树：

• 若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
• 若任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
• 任意节点的左、右子树也分别为二叉查找树；
• 没有键值相等的节点。

平衡二叉搜索树（Self-balancing binary search tree）

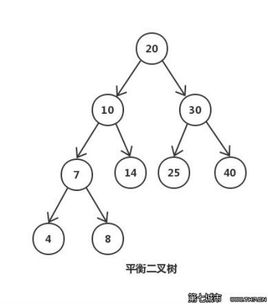
又被称为AVL树（有别于AVL算法），且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

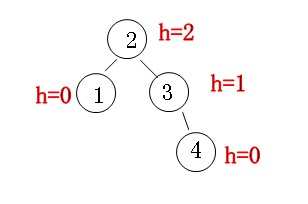
平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。

最小二叉平衡树的节点总数的公式如下 F(n)=F(n-1)+F(n-2)+1 这个类似于一个递归的数列，可以参考Fibonacci(斐波那契)数列，1是根节点，F(n-1)是左子树的节点数量，F(n-2)是右子树的节点数量。

红黑树

虽然本质上是一棵二叉查找树，但它在二叉查找树的基础上增加了着色和相关的性质使得红黑树相对平衡，从而保证了红黑树的查找、插入、删除的时间复杂度最坏为O(log n)。

红黑树的5个性质：

• 每个结点要么是红的要么是黑的。
• 根结点是黑的。
• 每个叶结点（叶结点即指树尾端NIL指针或NULL结点）都是黑的。
• 如果一个结点是红的，那么它的两个儿子都是黑的。
• 对于任意结点而言，其到叶结点树尾端NIL指针的每条路径都包含相同数目的黑结点。

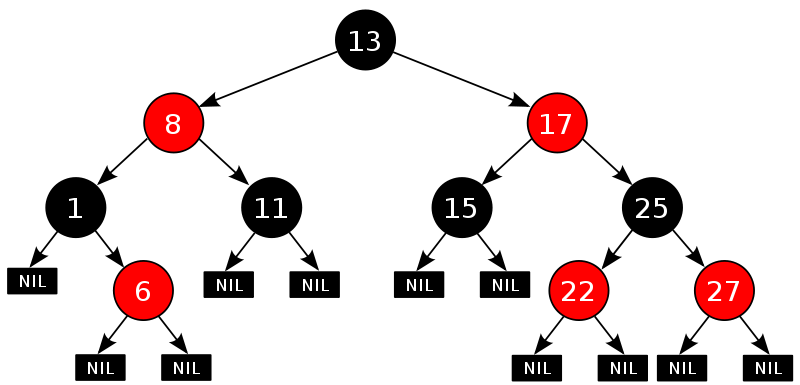
这些约束确保了红黑树的关键特性：从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例，这个在高度上的理论上限允许红黑树在最坏情况下都是高效的，而不同于普通的二叉查找树。